数学被鬼附身了

在过去的几个月里，我写了很多 Lean 代码。

Lean 是一门编程语言，但它主要被数学家使用。这很不寻常！这是因为 Lean 旨在将数学形式化。

Lean 让数学家可以像写代码一样对待数学——把数学拆分为结构、定理和证明，相互导入彼此的定理，并上传到 GitHub。

核心思想是，也许有一天，人类的大部分数学知识都可以以代码的形式存在——静态检查、可验证、可组合。

那么，使用 Lean 是什么感觉呢？

抱歉但不抱歉

为了让你感受一下 Lean，这里有一个极小的定理，声明 2 等于 2：

theorem two_eq_two : 2 = 2 := by
  sorry

这里发生了什么？

在数学家的眼中，这种语法看起来像是在陈述一个定理。我们有 theorem 关键字、定理的名字、一个冒号 : 后面是定理的内容、我们想要证明的陈述，以及 := by 后面跟着证明（sorry 表示我们还没有完成实际的证明，计划以后补上）。

但如果你是程序员，可能会注意到别的东西。那个 theorem 看起来很像函数。但 2 = 2 又是什么？它看起来像是函数的返回类型。但 2 = 2 怎么会是类型呢？难道 2 = 2 不是布尔值吗？如果 2 = 2 真的是类型，那这个 2 = 2 类型的值又是什么？这些都是很有趣的问题，但我们暂且先不深究。

我们先来看看这个证明：

theorem two_eq_two : 2 = 2 := by
  sorry

（你可以在 在线编辑器 里试试，虽然比不上 本地配置，但也能体验下。）

把光标放在 sorry 前面，右侧会有一个叫 Tactic state 的面板。此时，tactic state 显示 ⊢ 2 = 2：

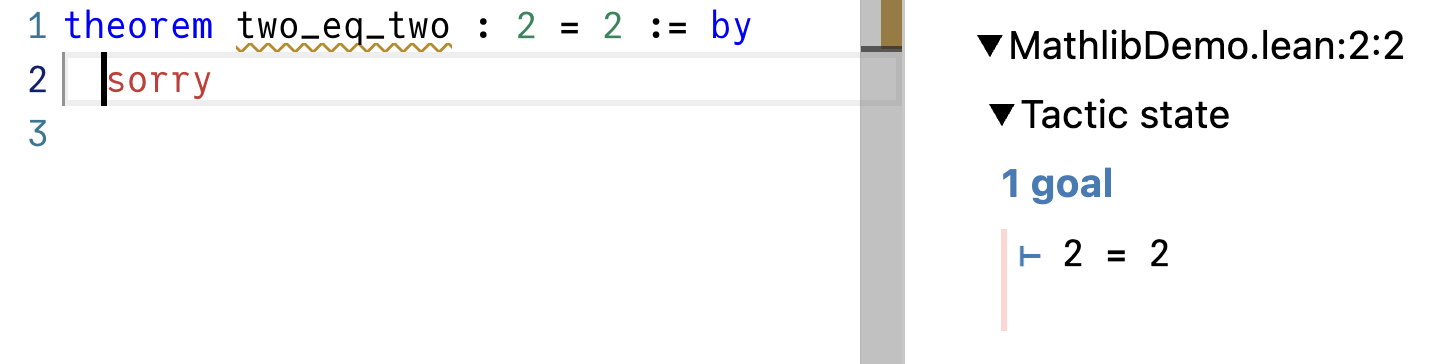
这里，⊢ 表示目标，也就是你要证明的陈述。你当前的目标就是证明 2 = 2，所以 tactic state 显示 ⊢ 2 = 2。

现在把光标放到 sorry 后面，会发现目标消失了：

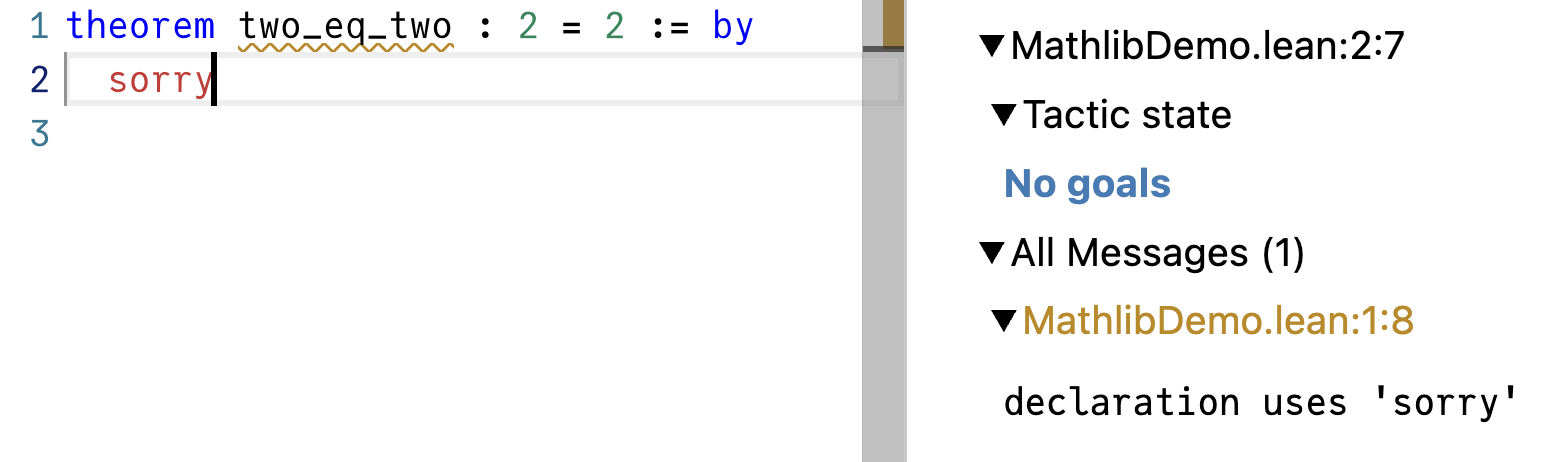
目标没了！换句话说，你通过写 sorry“证明”了 2 = 2。

当然，这毫无意义。你可以把 sorry 看作万能证明——它可以关闭任何目标。这是个谎言。从这个意义上说，sorry 就像 TypeScript 里的 any。它让你绕过证明检查器，但你实际上什么都没证明。

我们来试着去掉 sorry：

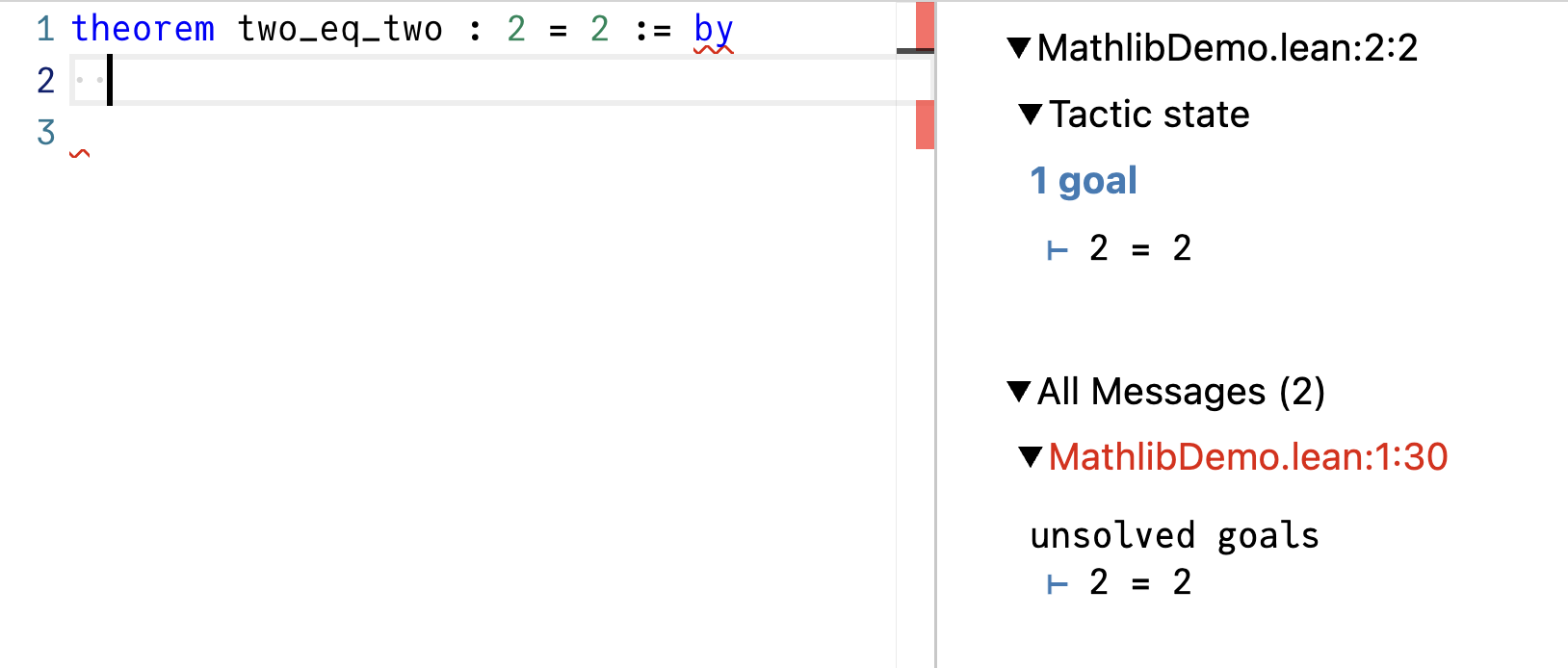
现在你会看到证明不完整，目标也没有被解决。要真正证明 2 = 2，在下一行输入 rfl，就能成功关闭目标：

这里，rfl 意为“反身性”（reflexivity），来自“反射”，就像镜像一样。只要你遇到“镜像”目标，比如 something = something，rfl 就能关闭它。你可以把 rfl 理解为内置的知识：“一个东西等于它自己”。

目标关闭后，你的证明就完成了。

theorem two_eq_two : 2 = 2 := by
  rfl

现在你已经证明了 two_eq_two，可以在其他地方引用这个事实。

theorem two_eq_two : 2 = 2 := by
  rfl
 
theorem two_eq_two_again : 2 = 2 := by
  exact two_eq_two

啊，模块化！

这里，two_eq_two_again 把证明的工作交给了 two_eq_two，因为当前目标（⊢ 2 = 2）正好就是 two_eq_two 已经证明的内容。（对于程序员来说，这看起来就像返回了一个函数调用的结果。）

虽然这个例子很简单，但 exact some_other_theorem 在拆分复杂证明时非常有用，可以把大证明分成小定理逐步完成。

我们用到的这些命令——exact、sorry、rfl——被称为战术（tactics）。Lean 的证明（by 后面）就是一系列战术的组合。战术让你关闭不同的目标——rfl 用于 x = x，exact some_other_theorem 用于你已经证明过的目标，sorry 可以关闭任何目标（但风险自负）。

要证明一个定理，你需要用恰当的战术直到所有目标都被关闭。

数学被鬼附身了

到目前为止，你已经证明了 2 = 2，这并不有趣。

我们来试试能不能证明 2 = 3：

theorem two_eq_two : 2 = 2 := by
  rfl
 
theorem two_eq_three : 2 = 3 := by
  sorry

和之前一样，sorry 可以关闭任何目标，哪怕是 2 = 3：

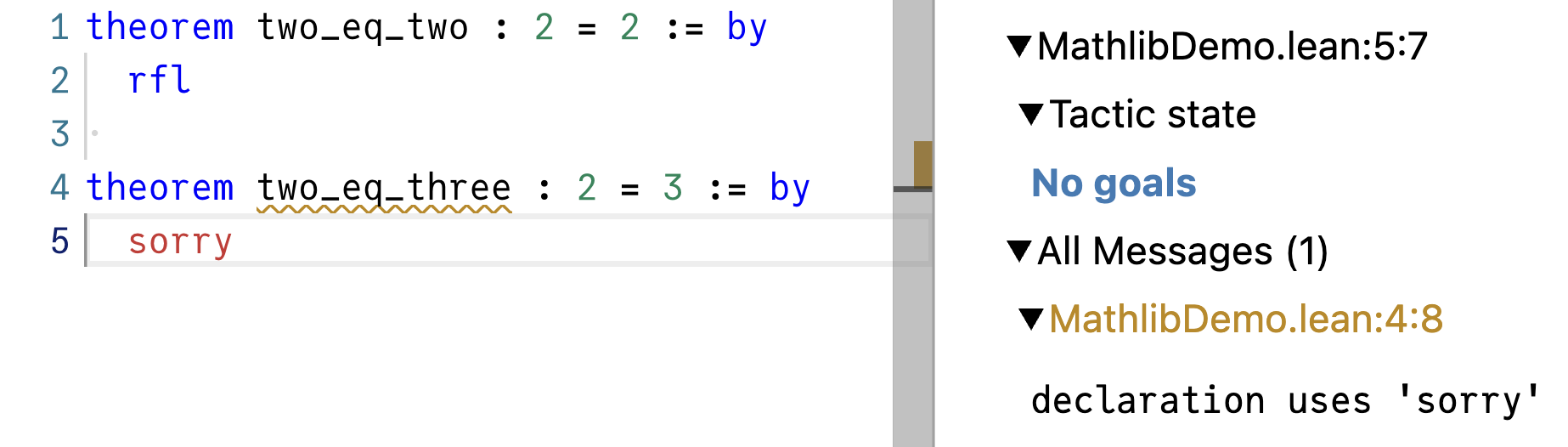
但这显然是作弊，我们还是想办法去掉 sorry。

把 sorry 换成 rfl：

这下可没那么容易了！你可以用 rfl 关闭 ⊢ 2 = 2，因为 2 = 2 形如 something = something。但目标 ⊢ 2 = 3 不是这种形式，所以 rfl 无法关闭 ⊢ 2 = 3。

其实，这正是好事。 在大多数有用的数学理论中，2 = 3 是假命题，我们不希望 Lean 能证明假命题。

但其实，数学并不是一成不变的。数学是你自己定义的。如果你愿意，你可以让数学“闹鬼”，让 2 = 3 成立。

我们来引入一个公理，声明这一点：

axiom math_is_haunted : 2 = 3

axiom 就像 theorem，但它是凭信仰接受的。你可以把它看作 theorem math_is_haunted : 2 = 3 := by sorry，但更理直气壮。

现在你可以在其他证明中把这个 axiom 当作事实使用：

theorem two_eq_two : 2 = 2 := by
  rfl
 
axiom math_is_haunted : 2 = 3
 
theorem two_eq_three : 2 = 3 := by
  exact math_is_haunted

注意，这并不会报错！

这里，two_eq_three 的目标正好和 math_is_haunted 公理的陈述一致，所以我们用 exact 战术来关闭目标。

有了 math_is_haunted 和一些战术，你甚至可以证明更“邪门”的东西。比如，我们来证明 2 + 2 其实等于 6：

theorem two_eq_two : 2 = 2 := by
  rfl
 
axiom math_is_haunted : 2 = 3
 
theorem two_add_two_eq_six : 2 + 2 = 6 := by
  -- 我们将在这里写点什么（顺便说一句，这是一条注释）

我们一开始的目标是 ⊢ 2 + 2 = 6：

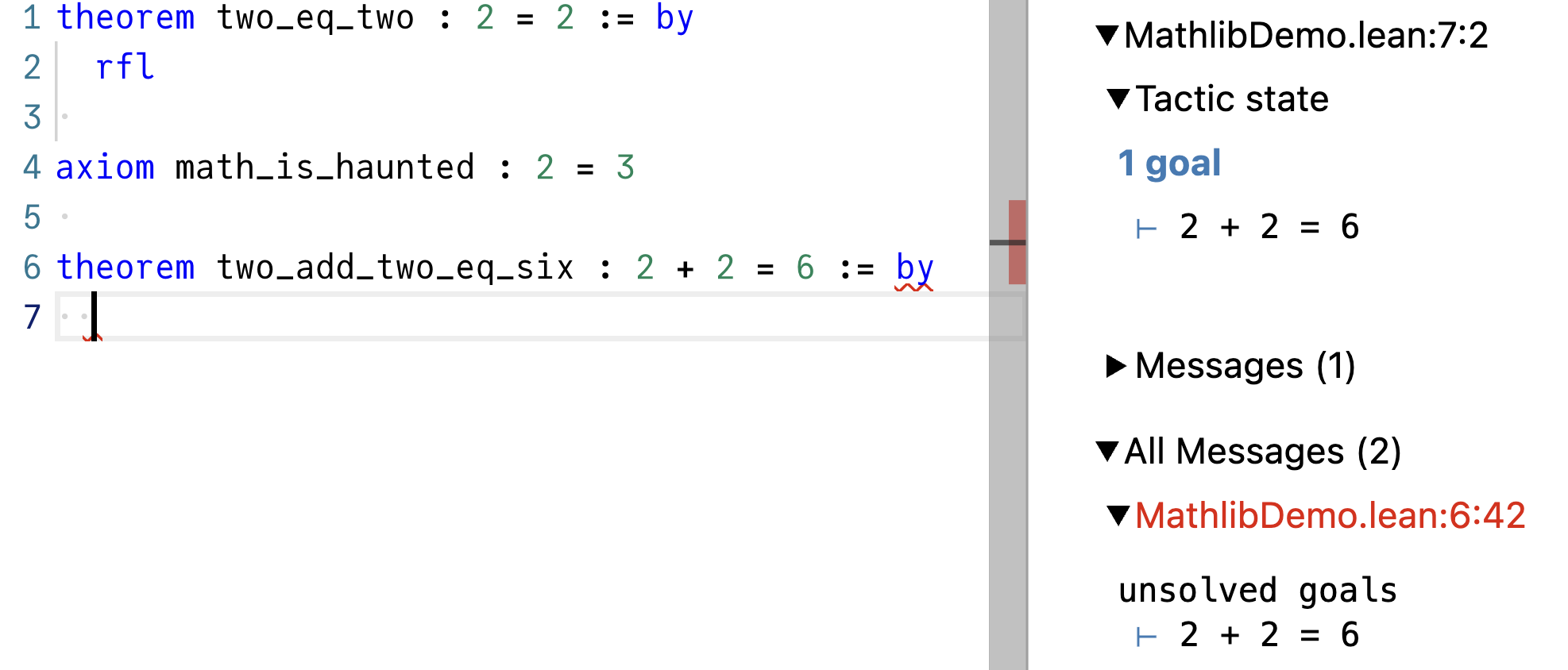
我们没有能直接解决这个目标的战术。但我们有 math_is_haunted，它“证明”了 2 = 3。如果 2 真等于 3，那么要证明 2 + 2 = 6，只需要证明 3 + 3 = 6。

rewrite 战术可以帮我们做到这一点——把目标里的每个 2 都替换成 3：

我们还是有一个未解决的目标，不过现在变成了 ⊢ 3 + 3 = 6。

rewrite 战术就像在目标里“查找并替换”。如果你有一个 a = b 的证明，把它交给 rewrite，目标里的所有 a 都会变成 b。由于 math_is_haunted “证明”了 2 = 3，rewrite [math_is_haunted] 就把目标从 ⊢ 2 + 2 = 6 变成了 ⊢ 3 + 3 = 6。

现在我们的目标是 ⊢ 3 + 3 = 6，这就容易多了。实际上，rfl 战术就能关闭这个目标，从而完成整个证明：

theorem two_eq_two : 2 = 2 := by
  rfl
 
axiom math_is_haunted : 2 = 3
 
theorem two_add_two_eq_six : 2 + 2 = 6 := by
  rewrite [math_is_haunted]
  rfl

（这里，rfl 能关闭 ⊢ 3 + 3 = 6，但原因可能和你想的不一样。它其实并不“知道” 3 + 3 是 6。实际上，rfl 会把两边的定义都展开再比较。当 3、6 和 + 被展开后，两边都会变成类似 Nat.zero.succ.succ.succ.succ.succ.succ 的形式。所以这其实还是个 something = something 的情况，rfl 就能关闭它。）

这样一来，我们就“成功”证明了 2 + 2 = 6。

这是不是有点毛骨悚然？事实上，math_is_haunted 这个公理太邪门了，它甚至能推导出矛盾（比如 2 + 2 = 6 和 2 + 2 ≠ 6 可以同时被证明），按照逻辑的规律，这意味着我们现在什么都能证明了。

在这里，是我们自己故意加了 math_is_haunted，所以这也怪不得别人。但实际上，上世纪初还真发生过类似的事。人们发现，构建大部分数学的集合论中有一个矛盾源自某个公理。后来通过选择不同的公理“修补”了这个问题，但这也让数学界陷入了焦虑、脱发和灵魂拷问。

现在我们把 axiom math_is_haunted 删掉。这样一来，依赖这个邪门公理的 two_add_two_eq_six 证明就坏了：

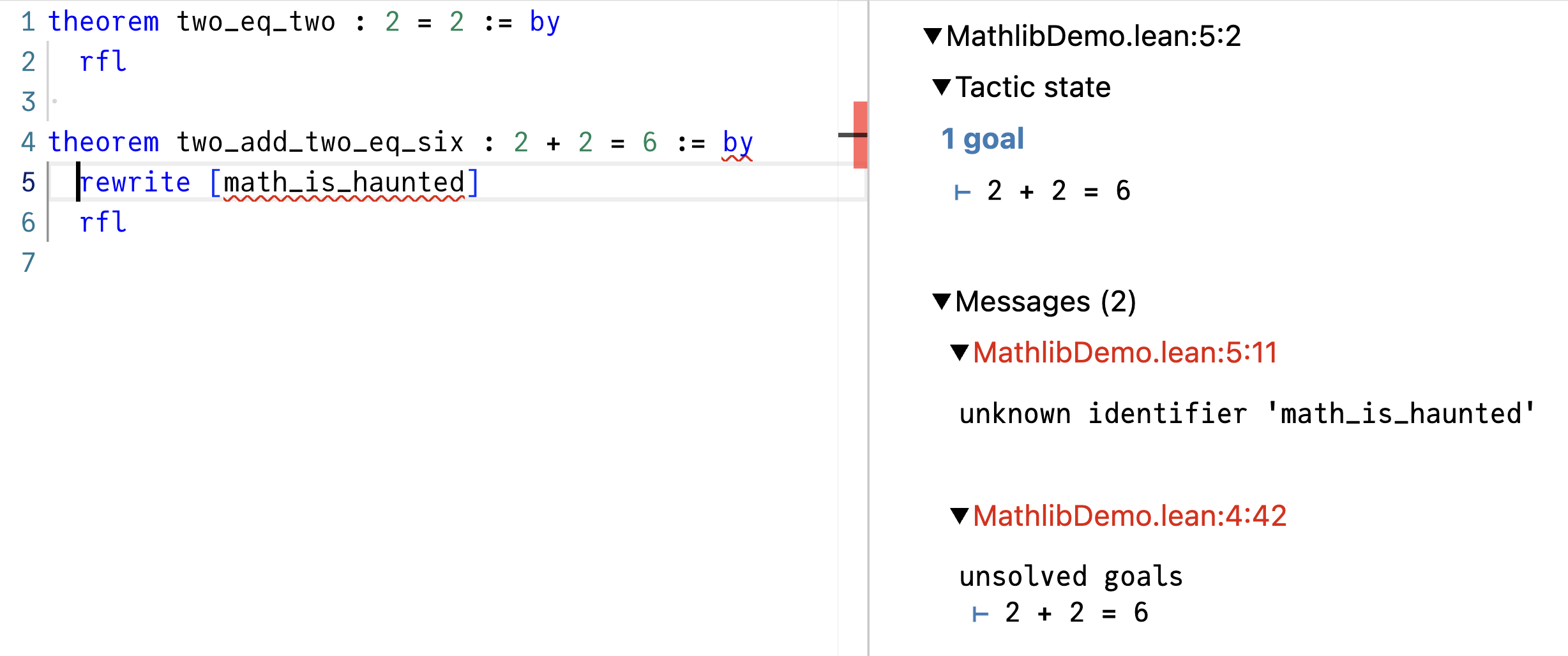
这正是我们想要的！坏掉的东西就不应该能通过证明检查。

要修复它，我们把命题改成 2 + 2 = 4，这才是正确的（根据 Lean 所熟悉的自然数公理）：

没有了那个坏公理，数学就不再“闹鬼”了！（或者说，我们只能希望如此）

用“胡说八道的数学”来介绍 Lean 可能有点奇怪，毕竟大多数人在 Lean 里做的数学其实都很严肃。但我认为，这很有力地说明了和证明检查器打交道的本质。

证明检查器只验证你选定公理下逻辑推理的有效性。它让你用 rewrite、rfl、exact 以及更多战术，串联起各种逻辑变换，逐步证明越来越复杂的数学结构和定理。

只要你的公理是可靠的，Lean 本身也是可靠的，你的结论就可靠。无论你的证明只是一个 rfl，还是几百万行 Lean 代码，这都成立。

费马大定理

举个极端的例子，来看一下费马大定理。它说，对于任意大于 2 的 n，不存在三个正整数 x、y、z 满足 xⁿ + yⁿ = zⁿ。

import Mathlib
 
theorem PNat.pow_add_pow_ne_pow (x y z : ℕ+) (n : ℕ) (hn : n > 2) :
    x^n + y^n ≠ z^n := by
  sorry

这个定理在被提出后 350 多年，直到 1994 年才被证明，证明过程长达 100 多页。

现在有一个正在进行的项目，试图用 Lean 形式化这个定理的证明，预计将耗时数年。虽然命题本身很简单，但证明需要建立许多数学结构和定理。

如果你克隆 FLT 仓库并打开 FermatsLastTheorem.lean，你会看到一个证明，但它其实依赖了 sorry，可以通过打印它的公理看出来：

#print axioms PNat.pow_add_pow_ne_pow
/-
'PNat.pow_add_pow_ne_pow' depends on axioms: [propext, sorryAx, Classical.choice, Quot.sound]
-/

但等到所有子证明都被形式化，这个项目完成时，pow_add_pow_ne_pow 所依赖的证明就不会再有 sorry，#print axioms PNat.pow_add_pow_ne_pow 里也不会再出现 sorryAx。

我敢打赌，合并那个最终消灭所有 sorry 的 PR 时一定会非常爽！

下一步

显然，今天我们并没有证明什么有用的东西。看起来为了搞清楚 2 + 2 = 4 这样的小事要做很多工作。但，嗯……你应该也感受到了一点特别的东西。它有点像编程，又有点不一样。如果你对 Lean 感兴趣，我推荐几个资源：

• 先试试 自然数游戏，这是一个非常温和又有趣的 Lean 入门教程。顺便还能学到自然数到底是什么。
• Mathematics in Lean 的前几章很容易上手，也不要求数学背景。我觉得它们很适合熟悉基本战术。
• 我最喜欢的数学书 Tao 的《分析》，现在有了 Lean 伴侣，而且在 GitHub 上持续更新。
• Lean Zulip 社区的“new members”频道非常友好。

虽然我没打算写 Lean 入门教程（自然数游戏和 Mathematics in Lean 已经足够好了），但我大概率会写一些具体的“啊哈”时刻，比如我前面提到的“2 = 2 其实是一个类型”之类的话题。Lean 融合了数学和编程领域丰富历史中的许多令人脑洞大开的思想，我在重新发现这些内容时感到非常快乐。我希望有更多人能无目的地试试 Lean——它真的很有趣。

当然，这要看你是不是那种喜欢的人了。

Discuss on Bluesky  ·  Edit on GitHub